Retour au sommaire Photos
ou des maths sans une seule formule!
0- Avant propos
Il arrive de rater une
photographie par manque de lumière... La photo est bougée et devient
inutilsable.
Dans certains cas, il est légitime de vouloir la sauver.
Lors de discussions sur les NG (NewsGroups), GR, par malice a souvent montré une photo ratée représentant un chevreuil, prise avec une lumière trop faible... Le bougé est important, mais il est tentant d'essayer de l'éliminer.
Photo originale trainant sur les NG. (Copyrigth GhostRider)
Voyons s'il est possible de réparer cette image... (Cette tâche va faire partie de ma conquête de l'inutile.)
Dans certains cas, il est légitime de vouloir la sauver.
Lors de discussions sur les NG (NewsGroups), GR, par malice a souvent montré une photo ratée représentant un chevreuil, prise avec une lumière trop faible... Le bougé est important, mais il est tentant d'essayer de l'éliminer.
Photo originale trainant sur les NG. (Copyrigth GhostRider)
Voyons s'il est possible de réparer cette image... (Cette tâche va faire partie de ma conquête de l'inutile.)
1- Qu'est-ce qu'un bougé?
Le bougé d'une photo, n'est que la convolution d'une image nette par une information de bougé.
Exemple: prennons quelques étoiles brillantes (fictives ! car il caille dehors... il neige !) dans le ciel, en pose longue et à la main.
Supposons que le bougé soit défini par:
La photo obtenue sera:
(on voit déjà sur cette image le résultat des approximations!)
En gros chaque étoile est remplacée par le motif du bougé.
Il est tentant d'écrire un programme qui va rechercher le motif du bougé, et le remplacer par un point: on obtiendrait ainsi une image nette. Mais ce n'est pas si simple!
Prennons une photo théorique avec des étoiles, et des traces brillantes d'étoiles filantes, ou de satellites (fictifs):
Si on introduit le bougé, on obtiendra:
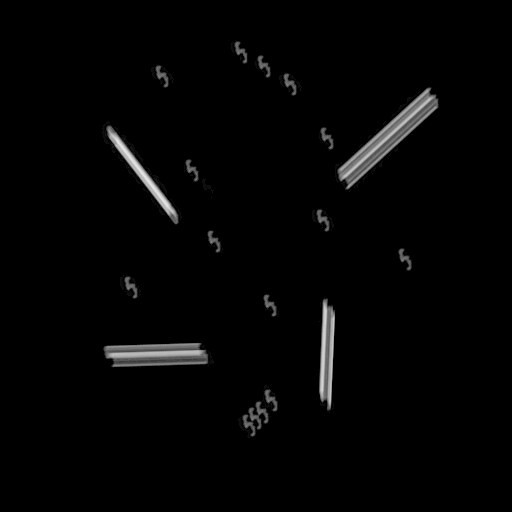
Là on se doute que récupérer les étoiles simples est encore facile, mais retrouver les traces satellites devient impossible, car les motifs se sont superposés.
Il existe une méthode en mathématiques pour faire ce traitement inverse: la déconvolution.
2- La déconvolution (sans maths)
Il est possible, en mathématiques, d'effectuer des changements d'espace, tant que le changement inverse existe et est unique. (C'est un peu comme passer une pensée du Français à l'Anglais. La pensée est la même, et pourtant on achangé de monde...)
L'espace de Fourier est ainsi souvent utilisé. Il s'agit de remplacer les données par des fréquences (soit en hertz soit en cycle/mm)
Ce qui est intéressant, c'est de remarquer que le bougé dans notre monde image, est remplacé par une simple mutiplication de Transformée de Fourier de l'image et du motif!
TF (image + bougé) = TF(image
non bougée) x TF(bougé)
Si on a une image bougée, et qu'on arrive à estimer le bougé, pour obtenir l'image non bougée, il faudra faire:
TF (image non bougée) = TF (image
+bougé) / TF(bougé)
Le calcul de la Transformée de Fourier Inverse de TF(image non bougée) donne l'image non bougée !
Le calcul de la Transformée de Fourier Inverse de TF(image non bougée) donne l'image non bougée !
Ainsi par des calculs complexes, on obtient une image non bougée.
Toute la difficulté consiste à estimer le mouvement avec le plus de précision possible. (et à faire les calculs !)
3- Exemple d'images et TF d'images
(dans les chapitres suivants, l'image réelle sera à gauche et sa TF à droite. Les médaillons décrivant un gros plan)
Champ d'étoiles:
Détail du motif étoile
Le masque:
détails du masque
Le champ d'étoiles bougés
On voit bien sur la dernière TF qu'on a le motif TF(champ étoiles) x TF(motif bougé)
4- Revenons à notre chevreuil
Conditions: Pour simplifier les calculs de Transformées de fourier, on va prendre une image carrée 512x512.
Que l'on va traiter en Noir et Blanc:
La déconvolution
(TF(flou)/TF(masque) donne:
La TF du masque ayant des pixels très noirs, la division par presque zéro donnent des anomalies blanches qu'on va supprimer...
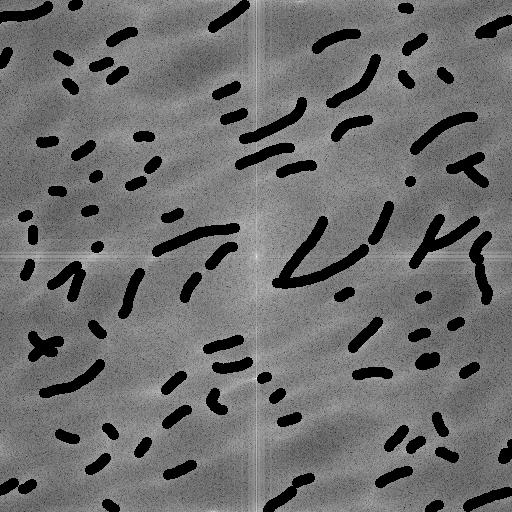
Qu'on traite ensuite pour corriger les dérives... (non normalisation des coefficients)
On peut voir ici que le bougé a (en partie) disparu. Mais le résultat reste grossier...
Causes pouvant expliquer le mauvais résultat:
- mauvaise estimation du bougé
- mauvaise définition de l'image
- masquage de la TF mal maitrisé
- absence de couleur
5- Et en couleur?
J'ai essayé le processus en traitant l'image en couleur:
- séparation des 3 couleurs RVB
- calcul de chaque déconvolution
- masquage des pics blancs (ici TF Rouge et Verte)
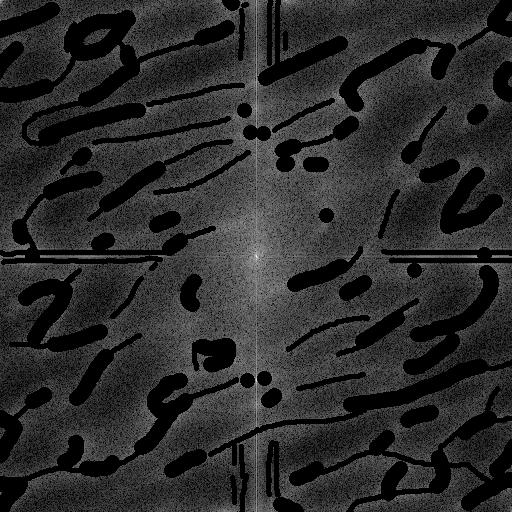
-TFI (R V B) et recomposition de l'image couleur
Les résultats sont décevants... franchement plats...
6- Et le gamma?
Et si j'avais oublié le gamma?
En effet, les images jpg sont dans un espace en gamma=0.45. Pour avoir une vraie linéarité, il faut passer dans un espace naturel et donc faire subir un gamma=2.2 à toutes les images... Faire les caculs de TF, déconvolution, et revenir dans un espace à gamma=0.45
- séparation des 3 couleurs RVB
- passage en espace naturel (application d'un gamma 2.2)
- calcul de chaque déconvolution
- masquage des pics blancs
- passage en espace gamma=0.45
- ajout de contraste (à la main)
Images R, V, B et finale
Pas si mal que ça (pour une bidouille!)
En effet, les images jpg sont dans un espace en gamma=0.45. Pour avoir une vraie linéarité, il faut passer dans un espace naturel et donc faire subir un gamma=2.2 à toutes les images... Faire les caculs de TF, déconvolution, et revenir dans un espace à gamma=0.45
- séparation des 3 couleurs RVB
- passage en espace naturel (application d'un gamma 2.2)
- calcul de chaque déconvolution
- masquage des pics blancs
- passage en espace gamma=0.45
- ajout de contraste (à la main)
Images R, V, B et finale
Pas si mal que ça (pour une bidouille!)
X- Conclusion
Seul le recours à l'artillerie
lourde
améliore le bougé!
Il s'agit ici de simples manipulations, avec beaucoup d'approximations... (bidouilles) Mais cela permet de comprendre comment on peut améliorer une image bougée.
Il faudrait, pour améliorer le procédé, avoir:
- des images mieux définies. (ici seulement 512x512)
- trouver une méthode pour mieux caractériser le bougé. Une meilleure image d'origine, permettrait également de caractériser le bougé avec plus de définition. Les calculs se feraient aussi moins "à la hache!"
- Voir si les images ont subi une rotation de bougé, car tout ce qui a été décrit ici, considère que le bougé est le même quelque soit les points de l'image.
- ne pas travailler en jpg, car c'est aussi un système qui utilise Fourier (DCT) et qui fait de mauvaises approximations... , en 8 bits.
- faire tous les calculs en 32 bits...
J'ai plein d'autres idées pour améliorer le procédé, mais est-ce bien utile? Il suffit de prendre des photos non bougées!
NB Je n'ai pas abordé un point important dans cette description... c'est pour voir si des gens vont lire ce document!
Merci à Ghost-Rider qui m'a prêté spontanément, sans le vouloir et sans le savoir son image de chevreuil, qui m'a permis de faire ces essais. (Depuis, j'ai obtenu son autorisation. Voir msg 2010-12-04 17h20)
A GR, je lui conseillerai de s'entrainer sur...
Ah, Ah, Ah! ;-)
Il s'agit ici de simples manipulations, avec beaucoup d'approximations... (bidouilles) Mais cela permet de comprendre comment on peut améliorer une image bougée.
Il faudrait, pour améliorer le procédé, avoir:
- des images mieux définies. (ici seulement 512x512)
- trouver une méthode pour mieux caractériser le bougé. Une meilleure image d'origine, permettrait également de caractériser le bougé avec plus de définition. Les calculs se feraient aussi moins "à la hache!"
- Voir si les images ont subi une rotation de bougé, car tout ce qui a été décrit ici, considère que le bougé est le même quelque soit les points de l'image.
- ne pas travailler en jpg, car c'est aussi un système qui utilise Fourier (DCT) et qui fait de mauvaises approximations... , en 8 bits.
- faire tous les calculs en 32 bits...
J'ai plein d'autres idées pour améliorer le procédé, mais est-ce bien utile? Il suffit de prendre des photos non bougées!
NB Je n'ai pas abordé un point important dans cette description... c'est pour voir si des gens vont lire ce document!
Merci à Ghost-Rider qui m'a prêté spontanément, sans le vouloir et sans le savoir son image de chevreuil, qui m'a permis de faire ces essais. (Depuis, j'ai obtenu son autorisation. Voir msg 2010-12-04 17h20)
A GR, je lui conseillerai de s'entrainer sur...
Ah, Ah, Ah! ;-)
Une nouvelle déconvolution a été lancée quelques jours plus tard, les résultats se sont améliorés. Voir Deconv2.php
JMP, le 4 et 6 décembre 2010
Copyright JM Pichot. Toutes les photographies de cette page ou de mon site, sont ma propriété exclusive.
Il est interdit de les copier ou de les utiliser sous quelque support que ce soit, sans mon consentement.
Edition originale 2010-12-04, rev2;